Parallel Phase Field Method
Summary:
The Phase-Field method is a mathematical technique, based in thermodynamics, for describing the process of phase transition in a material (e.g. from a liquid to solid). One of the distinguishing characteristics of the phase field approach is that the interface between phases is diffuse. This is in contrast to methods which assume a sharp interface between phases, that is, each point in the material is either fully solid or fully liquid, with the interface describing a moving 2-dimensional surface, complete with associated boundary conditions. The phase-field is an order parameter introduced to the model which holds the phase value, from 0.0 (pure liquid) to 1.0 (pure solid), for each point in the volume of material. Although the phase-field does not necessarily correspond directly to some physical material parameter (although it can), the introduction to the model of this order parameter is a useful mathematical technique commonly used in material science. The phase field method reduces to the sharp interface picture of a phase transition in the limit where the interface thickness goes to zero.
One advantage gained by using the phase-field method to model phase transitions, compared to the more commonly used sharp-interface method, is that the explicit tracking of the moving surface, the liquid and solid interface, is completely avoided. Instead, the phase of each point in the simulated volume is computed at each time step. The liquid-solid interface can be determined, and viewed, after the computation completes by post-calculating isosurfaces of constant phase field (say at a value of 1/2). In addition, the phase field method incorporates many types of physical phenomena without ad hoc introduction.
Additional Technical Details:
In contrast to the sharp-interface method, the phase-field method updates the state of every point in the simulated volume on each iteration. This requires the use of full 3-dimensional arrays to hold the phase field as well as other modeled parameters. This results in a large memory requirement for a phase-field method based simulator. For full resolution 3-dimensional simulations, the size of the computational grid over which these phase-field simulations are run can require a large amount of memory, 50 GB to 100 GB, as well as a large number of floating point computations per time step.
Single processor computers and small SMPs with 16 to 32 processors simply do not contain enough main memory to hold these computations, so a parallel version is necessary. It is this large memory requirement that has, until recently, prevented the regular use of the phase-field method. Now that large parallel machines and clusters have become commonly available this method has become feasible.
The simulator we have developed, which uses the phase-field method for modeling the solidification of an alloy, is implemented as a portable parallel C program using MPI (Message Passing Interface) for interprocessor communication.
The 3-dimensional arrays used in this simulator are distributed over the available processors such that each processor can complete one iteration of the simulation in approximately the same amount of time as the other processors. In the simplest case, if all processors are equally powerful and equally loaded, the array elements can be distributed evenly among the processors. Our implementation distributes the arrays in blocks along one axis although two or three dimensional distributions are possible. At the end of each iteration, processors holding adjacent array elements exchange those elements for use in the computation of the following iteration.
The load balance between the processors is monitored within the application and the distribution of the arrays is adjusted, between iterations, whenever a significant imbalance is detected. Both the frequency of these load balancing operations and the threshold of what is considered a "significant" load imbalance is easily configured by the user.
The distribution and load balancing of the arrays as well as the exchanging of neighboring array elements is managed by the routines in the utility library DParLib, an MPI (Message Passing Interface) based library for simplifying the coding of data-parallel style programs.
Performance Tests
Our dendritic growth simulator, bin3d, has been run on all of our local parallel machines and exhibits excellent performance and scales well as we increase the number of processors used for a given simulation size. The simulation updates each point in a uniform 3-dimensional grid of points using a simple finite-difference approximation to the partial differential equations that describe the system.
The bin3d simulator uses 8 3-dimensional arrays of size (nxnxn), each holding double precision floating point values. A near term goal is to perform simulations on grids of size 1000x1000x1000. Figure 1 shows the resulting per-processor memory requirement as a function the number of processors used for n=500 and n=1000.
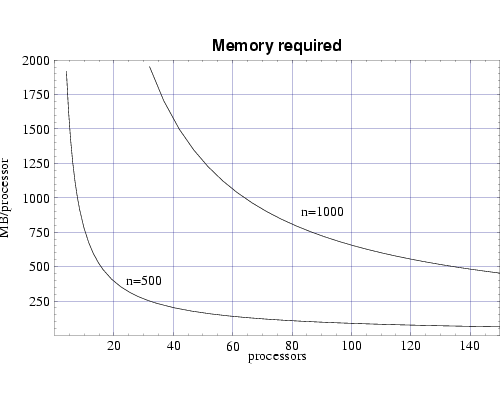
Fig 1: Memory requirement per node for bin3d.
An analysis of the bin3d algorithm shows that the expected run time for this simulator is O(n4). where the computational grid is of size n3. This reflects the fact that each grid point is updated on each time step of the simulation, for an order n3 computation on each iteration, and the number of iterations required for the liquid-solid interface to reach the edge of the volume increases linearly with n. Assuming a perfect speedup with the number of processors, this expected execution time T can be modeled with the equation:
![]()
where n is the number of computational grid points along each of the three axes, and p is the number of processors used.
Using several sets of test runs on our local machines, including an IBM SP with 200 MHz POWER3 processors, and a Beowulf cluster of 333 MHz Pentium II processors, we have plotted actual execution times against a curve fitted to our expected performance model T(n,p).
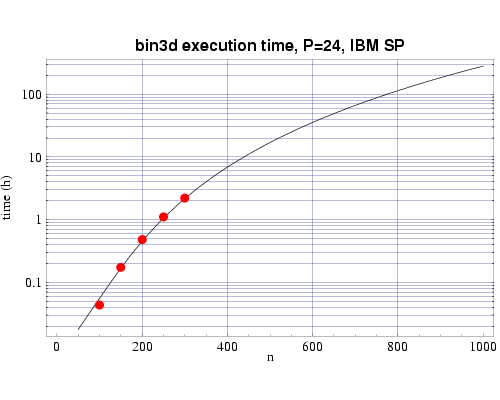
Fig 2: Execution time on 24 200 MHz POWER 3 processors. The plotted points are actual times and the curve fitted to the T(n,p) function.
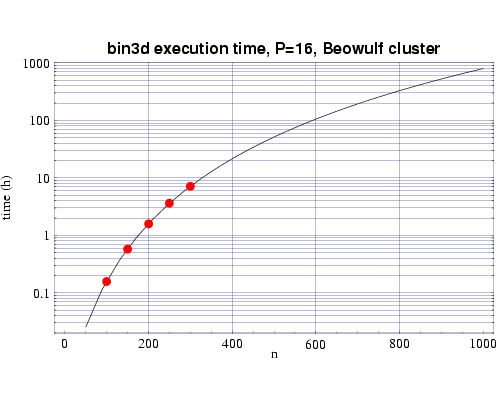
Fig 3: Execution time on 16 333 MHz Pentium III processors. The plotted points are actual times and the curve fitted to the T(n,p) function.
Using the T(n,p) functions determined from Figs. 2 and 3, we next show the results from a series of timing tests for a fixed problem size of n=250 and a varying number of processors. These results are plotted along with the prediction from the corresponding T(n,p) function we previously determined. These results, which show good agreement with the predicted values, are shown in Figs. 4 and 5. Some error begins to occur as the ratio of n/p begins to get too small and the communication overhead begins to become significant compared to the computational load on each processor.
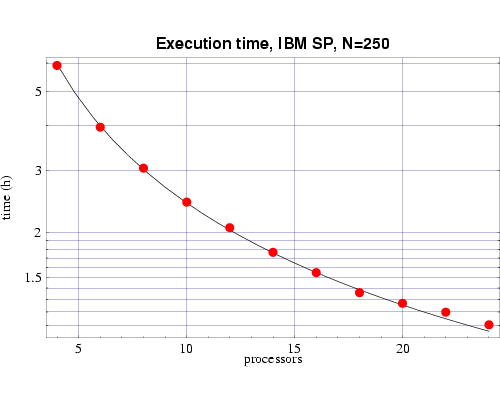
Fig 4: Execution time, on 200 MHz IBM POWER 3 processors, for bin3d with n=250. The plotted points are actual times and the curve is the function T(n,p) from Fig. 2.
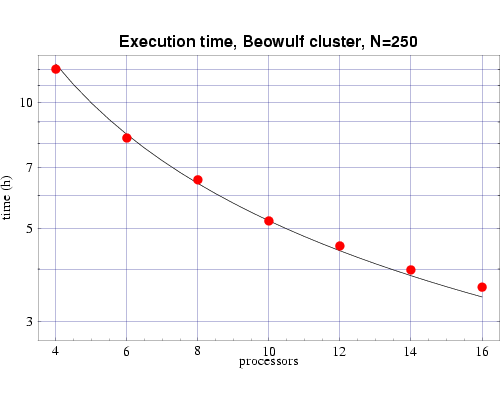
Fig 5: Execution time, on 333 MHz Pentium III processors, for bin3d with n=250. The plotted points are actual times and the curve is the function T(n,p) from Fig. 3.
Finally, we use the T(n,p) functions to predict the execution time for our target problem of n=1000 on both the IBM SP and on the Beowulf cluster of PCs. Assuming each processor has 1 GiB of main memory, and from the memory requirement plot in Fig. 1 we see that we need to use at least 70 processors to perform our full sized simulation. Figures 6 and 7 shows that this simulation, using 70 processors, would require approximately 4 days to complete on the IBM SP and approximately 10 days on the PC cluster. Of course these times will be be reduced as we upgrade the processing nodes in our parallel machines to more current technology and also if we simply use more processors.
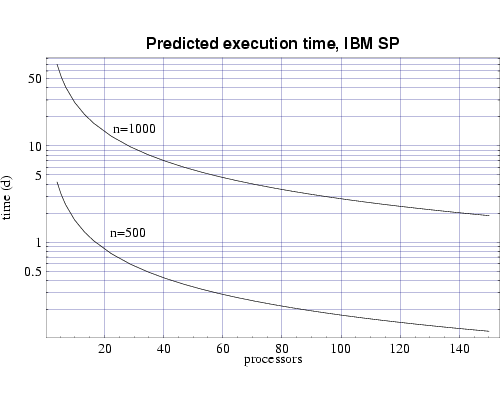
Fig 6: Predicted execution time for bin3d on 200 MHz IBM POWER 3 processors for problems of size n=500 and n=1000.
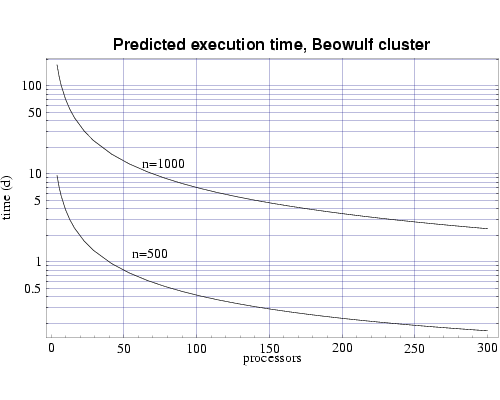
Fig 7: Predicted execution time for bin3d on 333 MHz Pentium III processors for problems of size n=500 and n=1000.
Applications:
- Modeling dendritic growth in metalic alloys
Return to High Performance Computing

