Summary
Modern instruments tend to produce data that are consisted of measured spectra, probability distribution functions, or simply sampled curves. Statistical methods such as ANOVA may be adapted and extended to analyses of such highly multivariate data. Recent developments in statistical methods for functional data analysis and high-dimensional data should be brought into bear on measurement problems. In fact, the nicely designed experimental data setting in typical NIST problems allows new statistical tools to be developed for statistical inference such as hypothesis testing and confidence interval assignment which would, otherwise, be difficult to do in an observational setting.
Description
Assessment of measurement data often raises statistical inference questions which have not been adequately addressed in the statistical literature. For example, NIST scientists may encounter issues on whether two measurement techniques give arise to similar measurement curves, whether there is a given experimental effect when experimental conditions are deliberately changed, how to characterize the within- and between-setting experimental or physical variation in functional data, and how to characterize the common mean and assign uncertainty statement for functional data measurements. Lastly, there are interesting experimental design issues such as how to design measurement strategies for measuring response curves at a few selected locations when there are resource constraints or experimental measurement limitations.
Statistical techniques which we have found useful in addressing some of these questions include: smoothing spline method for functional variance estimation, functional t-tests using multiple comparison, permutation/bootstrap methods, Bayesian confidence intervals, and both parametric and nonparametric regression methods for interpolation.
Major Accomplishments
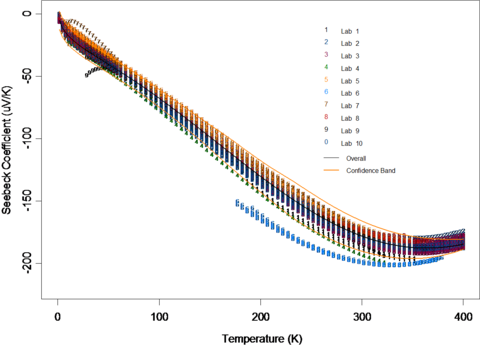
- Led the efforts in the statistical analysis of a round-robin measurement survey of two candidate materials for a Seebeck coefficient standard reference materials. A polynomial model is identified to represent the Seebeck coefficient as function of temperature, and statistical methods for irregularly sampled functional curves are developed based on ridge regression techniques. One of the several journal papers published related to this project is the NIST Journal of Research paper. The work led to production of NIST SRM 3451 on low temperature Seebeck coefficient and influenced many subsequent studies in the literature.
- Developed statistical methods for analysis of molecular mass distributional data (jointly with Charles Guttman, with assistance from Jennifer Huckett and Stephanie Wetzel). A manuscript was completed and is currently under revision based on editors' comments.
- Successfully applied functional data analysis techniques to several glass SRM certifications. Development of a splicing algorithm for combined use of SRMS for relative intensity correction standards for fluorescence spectroscopy.

