Unit Conversion

Unit conversion is a multi-step process that involves multiplication or division by a numerical factor, selection of the correct number of significant digits, and rounding. This multi-step process is presented in NIST SP 1038 - 2006 (Section 4.4), including a rounding procedure for technical documents, specifications, and other applications such packaged goods in the commercial marketplace and temperature. Common conversion factors are also listed (Section 5).

• Metric to U.S. Customary Conversions
• U.S. Customary to Metric Conversions
• NIST SP 811 – Appendix B (Current Edition) provides guidance on the use of conversion factors which are expressed using scientific notation (listed both alphabetically and by topic areas) and rules for rounding numbers and converted numerical values of quantities.
• NIST SP 1038 (Current Edition) lists the units of the International System of Units (SI), or metric system, recommended for use in trade and commerce and other general uses.
• NIST HB 44 – Appendix C (Current Edition) provides several convenient conversion factor tables for length, area, volume (dry and liquid measure), and mass using SI (metric system) and U.S. customary units, including notes on British measurement units.
• NIST HB 133 Appendix E (Current Edition) provides unit conversion factor tables for the benefit of those requiring a reference when checking the net contents of packaged goods.
• U.S. Survey Foot Revised Unit Conversion Factors
• Precious Metal Conversion Information
• Pressure and Gas Flow Conversion Information
• Metric Conversion Software
• US Metrication Resources
  • Errors and Mishaps may result when multiple measurement systems are simultaneously used.  
  • Best Practices - Resources are available for organizations systematically adopting the International System of Units (SI) within business systems and those analyzing the risks of working in hybrid or dual measurement environments.
  • Metric System Education - Learning the SI is not about making mental unit conversions (this will slow you down). Teach non-SI unit conversions only when required. Teach the metric system without making any comparisons to non-SI measurements. After students become proficient using the metric system and are comfortable applying SI measurements, they may encounter applications that require mathematical conversions between SI and non-SI units.

Dimensional analysis is a technique used to convert measurements. For example, changing the magnitude of a SI quantity or converting between SI and non-SI units. Some measurements have one dimension, for example length. A square shape (area) has two dimensions (e.g., length and width), while a cube (volume) has three dimensions (e.g., length, width, and height). Converting between measurement units is a very important skill when working within and between measurement systems.

This problem-solving method is based on the principle that quantities are defined as equalities. A conversion factor is an expression for the relationship between units that is used to change the units of a measured quantity without changing the value. A conversion ratio (or unit factor) always equals one (1), where the numerator and the denominator have the same value expressed in different units.

A numerator represents the parts out of the whole or how much you have. A denominator represents the total number of parts of the whole. In this example of the common fraction ¾, 3 is the numerator and 4 is the denominator. Performing the math calculation (3 divided by 4) transforms the number into a decimal fraction, 0.75.

This method uses the fact that any number or expression can be multiplied by "one" without changing its value. This allows the conversion of units by multiplying the initial measurement by one (or more) forms of the number 1. While the multiplication by 1 does not change the value of the measurement, it does change the measurement units.

Unit Conversion Process

This process uses the fact that any number or expression can be multiplied by "one" without changing its value. This allows the conversion of units by multiplying the initial measurement by one (or more) forms of the number 1. While the multiplication by 1 does not change the value of the measurement, it does change the measurement units.

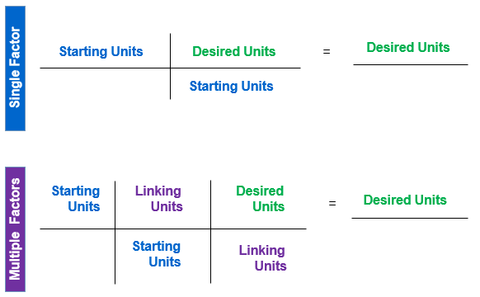
It’s very easy to systematically apply unit conversion process to solve conversions within or between measurement systems. It may be necessary to multiply by more than one conversion ratio in more complex conversions. Use these steps to construct a unit conversion problem so one (or more) of the units cancel until only the desired unit remains:

Step 1. Identify the unit you have. These are the Starting Units.

Step 2. Identify the unit you want. These are the Desired Units.

Step 3. Identify appropriate unit conversion factor(s). These are the Linking (or Ratio) Unit(s). Use EXACT conversion factors whenever available.

Step 4. Cancel units and perform the math calculations (e.g., multiply, divide). Repeat the calculation (double check).

Step 5. Evaluate the result. Does the answer make sense?

Best Practices

• Multiply the numerators (across) and denominators (across) to calculate an intermediate answer, then divide. Documenting the calculation steps can be especially helpful when problem-solving errors.
• Do not round any quantities used within the calculation.
• Only round the final calculated quantity.

Many unit conversion problems will require only a single unit conversion factor. However, multiple factors may be required to solve a problem. These figures illustrate both examples. Remember that Step 3, identifying the conversion factor, is often the most challenging step. If an incorrect (or approximate) conversion factor is used, a correct solution will not be achieved.

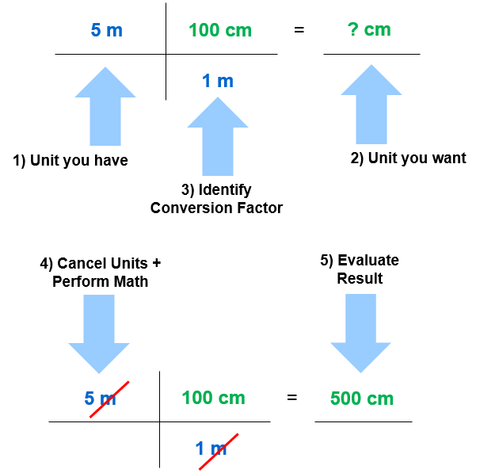
Example. An engineer has designed a new 5 m computer cable but must represent the length in centimeters within an owner manual diagram. How many cm is the length?