Gas properties for flow metering

Summary

Flow meters that rely on measuring the pressure drop across a laminar flow element can be accurately calibrated using a benign surrogate gas (such as helium or nitrogen) and then used to meter process gases (Wright et al., 2012), provided that accurate values of the surrogate-to-process-gas viscosity ratios are available.

Pope et al., 2012 demonstrated that the fluid-dependence of the complex calibration curves of turbine meters can be understood as a function of fluid's "kinematic viscosity", which is the ratio of the shear viscosity to the density. The database SEMIPROP can be used to calculate the densities of process gases from the virial equation of state and the NIST Chemistry WebBook provides densities of heat transfer fluids.

The gas flow through critical flow venturis (nozzles) depends upon the stagnation temperature and pressure upstream of the nozzle and on the real gas "critical flow function." (See Wright and Johnson, 2009). The real gas critical flow function is now available in NIST Standard Reference Database 23 (REFPROP), Version 9.1 or later.

Description

Schematic diagram of the two-capillary viscometer used by May et al.

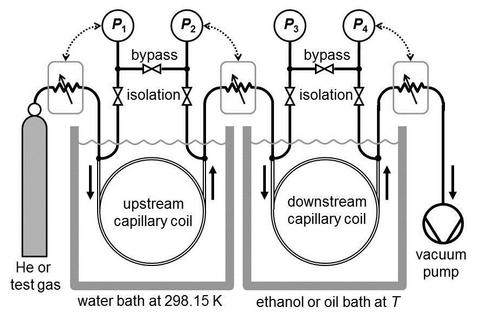
NIST has two on-line databases that include accurate gas viscosity values:

1. SEMIPROP - NIST Standard Reference Database 134 - for selected semiconductor process gases
2. NIST Chemistry WebBook - for heat transfer fluids, components of air, components of natural gas

[Note: as of February 2014, the NIST Chemistry WebBook provides data from Version 7 of "NIST Standard Reference Database 23 (REFPROP)"; The latest version of this database is for sale through NIST's Standard Reference Data program.]

The Fluid Metrology Group contributed highly accurate viscosity values to these databases using a novel, highly effective combination of theory, critical assessment of literature data, and direct measurements.

• Cencek et al., 2012 calculated the viscosity (and the thermal conductivity) of helium at zero density over the temperature range 1 K to 10,000 K. [see also supplementary material for tables of the thermophysical properties of helium.]. Their calculations use the fundamental constants of physics, quantum mechanics, and statistical mechanics. Their results had fractional standard uncertainties of 10−5 near ambient temperature; they are the smallest uncertainties for any gas viscosity.
• Berg and Moldover, 2012 critically reviewed published viscosity measurements for 11 dilute gases near 25 °C. The data from 18 instruments yielded viscosity ratios with fractional uncertainties ranging from 2.7×10−4 to 3.6×10−4. Using the theoretical value for helium as a reference, they recommended viscosities for these 11 gases with similar, small uncertainties. Their results are built into NIST Standard Reference Database 23 (REFPROP), Version 9.1 or later.
• May et al., 2007 and May et al., 2006 developed a two-capillary viscometer to measure the ratio of the calculated viscosity of dilute helium to the viscosity of test gases over the temperature range 200 K to 400 K. (See Figure.) In this temperature range, they determined the viscosities of dilute hydrogen, methane, argon, and helium. Their data were used to validate other instruments and to test calculated values of the viscosity of hydrogen and argon. If their data were reanalyzed using the recent helium viscosities from [Cencek et al] they would have uncertainties in the range 2×10−4 to 8×10−4.
• Gillis et al., 2003 developed an acoustic viscometer for measuring the viscosities of gases at pressures up to 3 MPa. (see Acoustic Techniques in Fluid Metrology) At NIST, Hurly used an acoustic viscometer calibrated with helium and argon to determine the viscosities of semiconductor process gases, alternative refrigerants, siloxanes, and mixtures of {helium + xenon}. Hurly's measurements have uncertainties of approximately 0.5%. They were published in the archival literature [9, keith.gillis [at] nist.gov (Subject: Reprint%20request) (10), keith.gillis [at] nist.gov (Subject: Reprint%20request) (11)] and in SEMIPROP - NIST Standard Reference Database 134.

The Fluid Metrology Group applied gas viscosity data and a physical model of the laminar flow meter (LFM) to improve the extrapolation of LFM calibrations from one gas to another. Wright et al., 2012 calibrated three models of commercially-manufactured, laminar flow meters at four pressures (100 kPa, 200 kPa, 300 kPa, and 400 kPa) with five gases (N2, Ar, He, CO2, and SF6) over a 10:1 flow range using NIST's primary flow standards as references. We combined three items: (1) the calibration data acquired with N2, (2) gas-property data from NIST's database REFPROP 9.0, and (3) a physical model for each LFM that accounts for the effects of viscosity, entrance and exit effects, gas expansion, gas non-ideality, and slip. This combination predicted the calibrations for the flow of Ar, He, CO2, and SF6 with a maximum error of 0.8% for Reynolds numbers Re < 500. Under these conditions, the present LFM model allows prediction of calibration results for other gases with approximately 3 times lower uncertainty than conventional approaches that plot the flow coefficient as a function of the viscosity coefficient or Re.